Alturas de un triángulo

 

Uno de los elementos más importantes de un triángulo es su altura. Un triángulo tiene tres alturas.

La altura es la menor distancia entre un vértice y el lado opuesto (o su prolongación), por lo que a cada vértice le corresponde una altura.

También utilizamos el nombre de altura para referirnos a la recta que pasa por un vértice y es perpendicular al lado opuesto, pues es sobre esta recta sobre la que medimos esa distancia.

Veamos como construir las alturas de un triángulo con Geogebra.

1.- Triángulo acutángulo

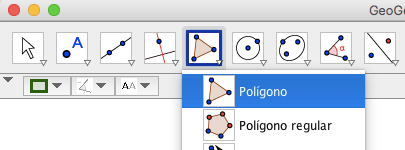
Seleccionamos la herramienta «Poligono»

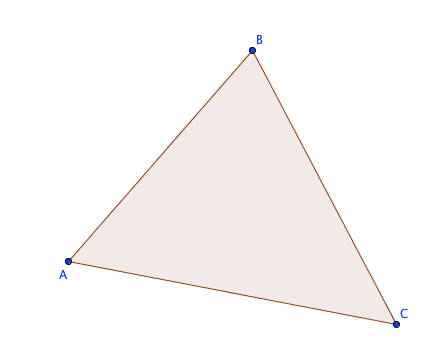
construimos un triángulo ABC

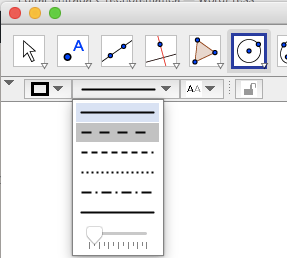
seleccionamos la herramienta «Circulo» y cambiamos a linea discontinua para usarla como elemento auxiliar en la construcción:

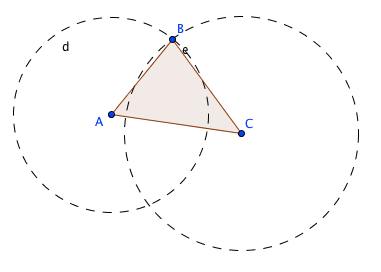
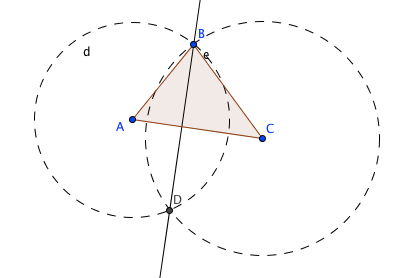
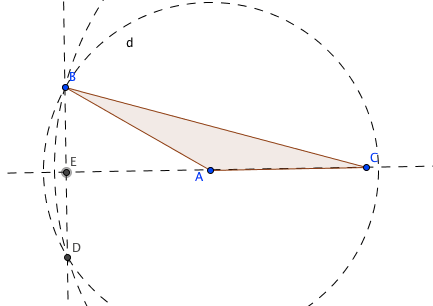
vamos a construir la altura desde el vertice B al lado AC , por lo tanto creamos dos circunferencias. La primera con centro en A y radio AB, la segunda con centro en C y radio CB

 

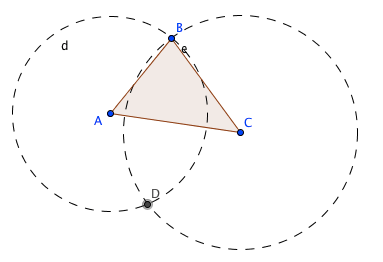
con la herramienta «Intersección» marcamos el punto de intersección de las circunferencias (D)

 

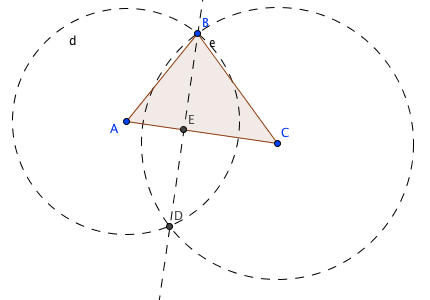
creamos una recta BD, 

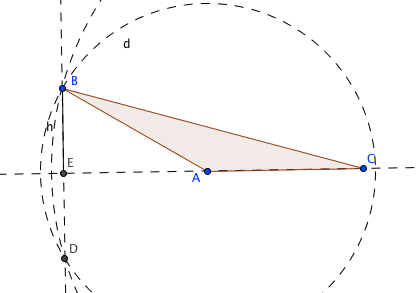
marcamos el punto de intersección de la recta BD con el lado AC del triángulo

cambiamos a línea discontinua la recta BD

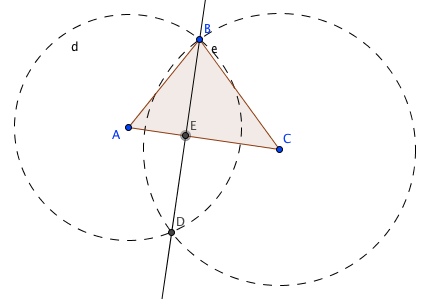
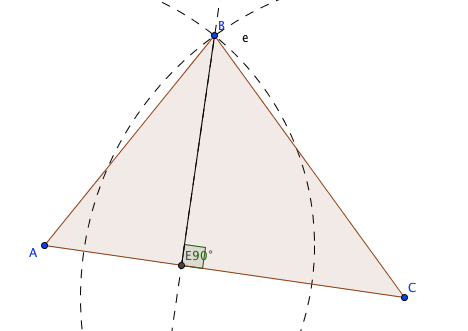
con la herramienta «Segmento» construimos un segmento BE

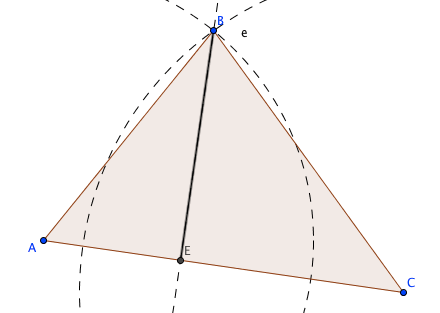
el segmento BE es la altura del vertice B al lado AC.  

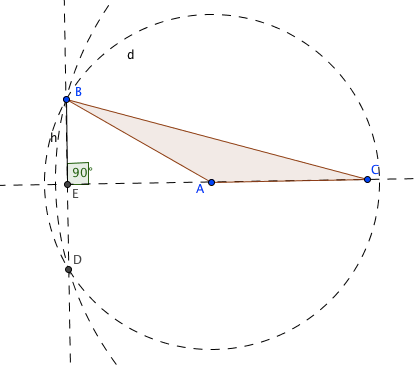
Comprobamos con la herramienta «Angulo»

midiendo en ángulo CEB

Como actividad construye las otras alturas.

2.- Triángulo obtusángulo

El triángulo obtusángulo es aquel que tiene un ángulo obtuso: es decir, que mide más de 90º.

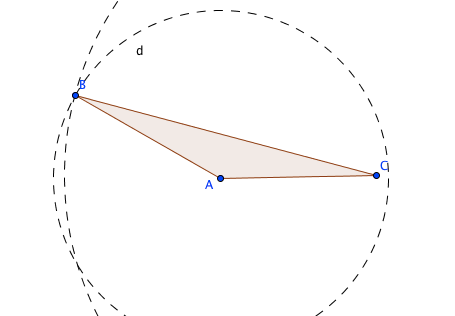
Creamos un triángulo obtusángulo ABC

seleccionamos la herramienta «Circulo» y cambiamos a linea discontinua para usarla como elemento auxiliar en la construcción, construimos la altura desde el vértice B al lado AC, por lo tanto creamos dos circunferencias.  La primera con centro en A y radio AB, la segunda con centro en C y radio CB

con la herramienta «Intersección» marcamos el punto de intersección de las circunferencias (D) y con la herramienta recta construimos la recta BD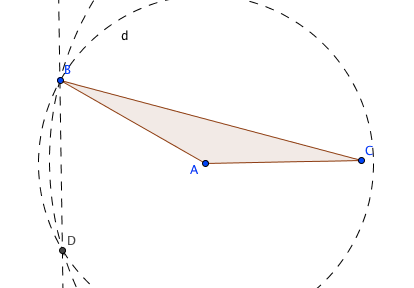

 

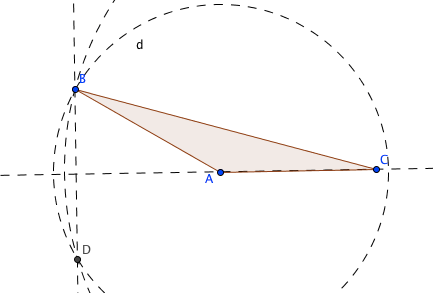
con la herramienta «Recta» prolongamos el lado AC del triángulo

marcamos la intersección de las rectas BD y la prolongación del lado AC, generando el punto E

ahora con la herramienta «Segmento» y con línea continua unimos los puntos BE

el segmento BE es una altura del triángulo ABC desde el vértice B al lado AC