¿Qué es Wolfram|Alpha?
Wolfram|Alpha es un buscador de respuestas Un buscador de respuestas no igual a los buscadores de Internet (como Google) en que éstos traen como resultado páginas o documentos que satisfacen una consulta, mientras que Wolfram|Alpha entrega respuestas haciendo un análisis que le permite dividir el problema para hacer consultas en diversas bases de datos, sintetizar conocimiento y presentarlo todo como la respuesta a la pregunta.
Wolfram|Alpha está escrito en Mathematica, que es un programa empleado para procesar datos de ingeniería, matemáticas y ciencias. Wolfram|Alpha tiene muchos usos, no únicamente los relacionados con cálculos científicos.
Existen versiones para iPad, iPhone, iPod Touch y dispositivos con Android. Para más detalle de sus especificaciones puedes ir a su página web Wolframalpha.com.
¿Como funciona?
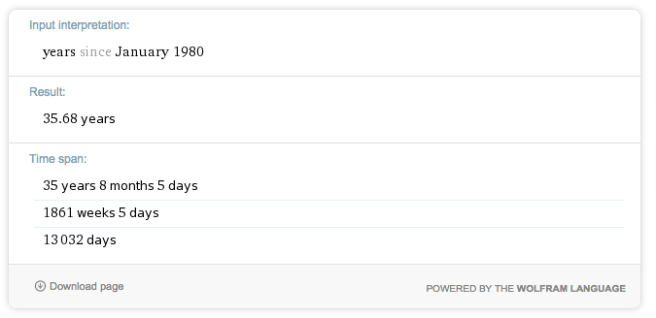
Wolframalpha responde preguntas escritas en inglés, por ejemplo: how many years from january 1980?
Es importante verificar la sección «Input interpretation» para ver si escribimos bien nuestra pregunta. Como se ve en la imagen dependiendo de la pregunta entrega varias respuestas.
Ejemplos
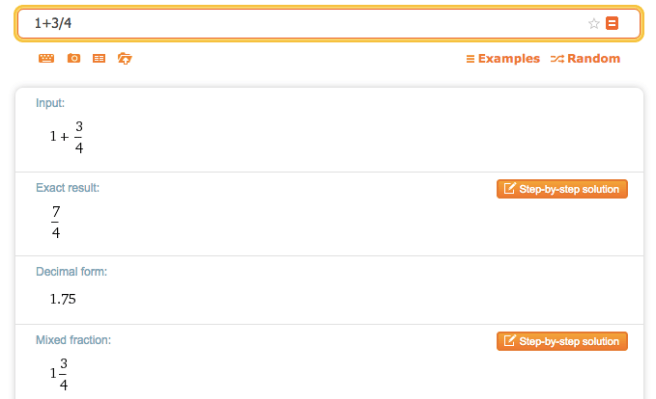
1.- Aritmética básica
2.- Reducción de términos semejantes:
Es importante ingresar las expresiones de forma correcta para que Wolframalpha pueda interpretar el problema y entregar una solución correcta. Veamos como ingresamos una expresión algebraica con exponentes.
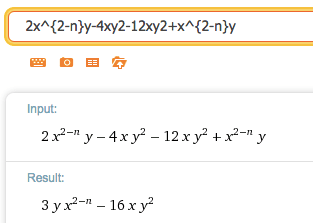
3.- Reducir la siguiente expresión:
Podemos colocar el símbolo «^» para indicar el exponente:
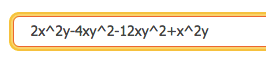
o simplemente escribirlo después del factor literal:
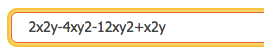
En cualquier caso la interpretación y respuesta es la misma:
Sin embargo a la hora de ingresar un expresión con exponente un polinomio es necesario utilizar el símbolo «^» con paréntesis.
4.- Reducir:
Resulta: